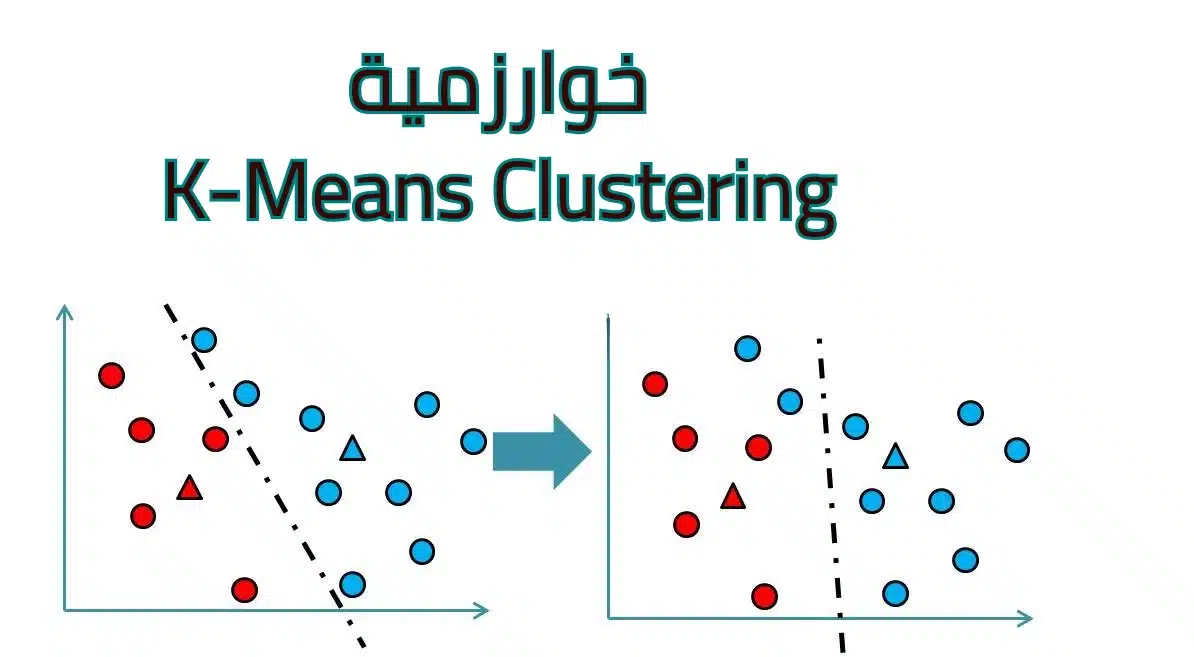
خوارزمية K-Means Clustering: أهم أدوات تحليل البيانات وتصنيفها
كيف تساعد خوارزمية K-Means Clustering في تصنيف البيانات وتحليلها؟
هل تساءلت يومًا كيف يمكن للشركات تحليل البيانات لتقديم تجارب مخصصة للعملاء؟ باستخدام خوارزمية K-Means Clustering، يمكن تقسيم العملاء إلى مجموعات بناءً على سلوكهم الشرائي، مما يساعد على تحسين استراتيجيات التسويق وزيادة الفعالية. وتُعتبر هذه الخوارزمية أداة قوية لتحليل البيانات غير الخاضعة للإشراف، وتستخدم في مجالات متعددة مثل التسويق، والرؤية الحاسوبية، وتحليل البيانات الجغرافية.
كيفية عمل خوارزمية K-Means Clustering
تبدأ خوارزمية K-Means Clustering بتقسيم البيانات إلى مجموعات تُعرف بالعناقيد. وتقوم الخوارزمية بتحديد عدد العناقيد K مسبقًا، ثم اختيار K مركزًا بشكل عشوائي. بعد ذلك، تعيّن الخوارزمية كل نقطة بيانات إلى أقرب مركز باستخدام المسافة الإقليدية. وعند اكتمال هذه المرحلة، تُحدث الوسائط لكل عنقود بناءً على متوسط نقاطه، وتُكرر العملية حتى تستقر العناقيد ولا تتغير النتائج بين الجولات.
اقرأ أيضا:
أخطاء هندسة الأوامر تدمر نتائج ChatGPT: صحّحها في 5 دقائق
50 سؤالاً وجواباً لفهم الذكاء الاصطناعي: كل ما تحتاج معرفته
المعادلة الرياضية
تهدف الخوارزمية إلى تقليل مجموع التباين داخل العناقيد باستخدام الصيغة الرياضية التالية:
argminS∑i=1k∑x∈Si∥x−μi∥2\arg \min_S \sum_{i=1}^k \sum_{x \in S_i} \|x – \mu_i\|^2argSmini=1∑kx∈Si∑∥x−μi∥2
حيث:
SiS_iSi: مجموعة النقاط في العنقود iii. μi\mu_iμi: المركز أو الوسيط للعنقود. ∥x−μi∥\|x – \mu_i\|∥x−μi∥: المسافة الإقليدية بين النقطة xxx والمركز μi\mu_iμi.
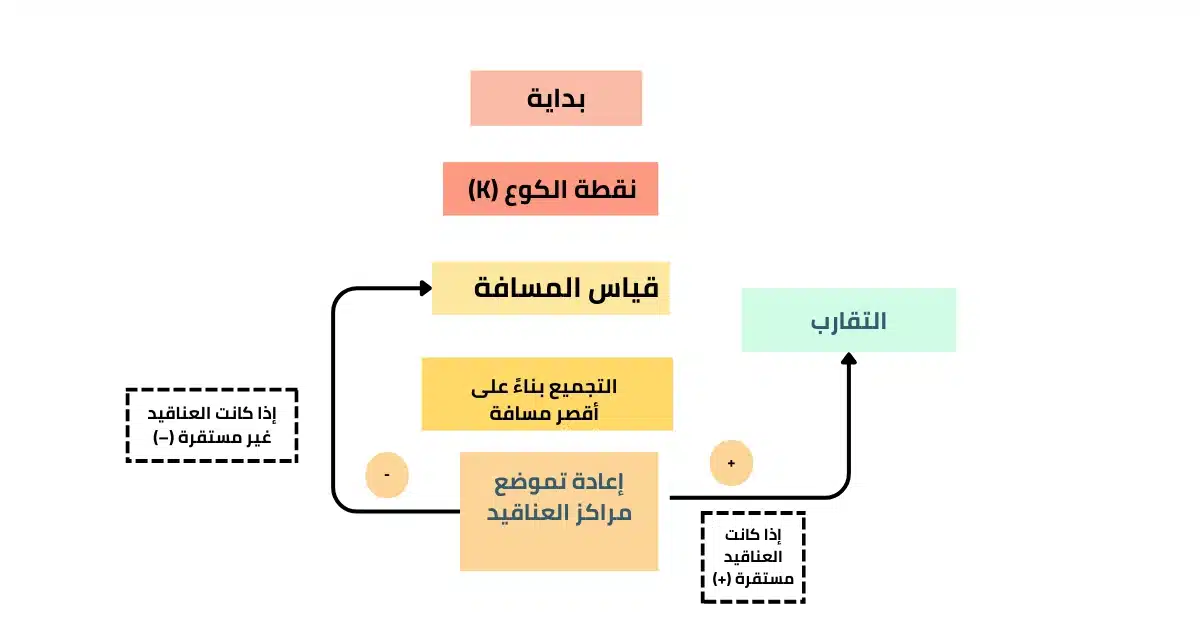
مزايا خوارزمية K-Means Clustering
تتمتع الخوارزمية بالعديد من المزايا، أبرزها:
- البساطة والسرعة: تعمل بشكل سريع حتى مع مجموعات البيانات الكبيرة.
- الوضوح: توفر نتائج سهلة الفهم والتحليل.
- التطبيق العملي: تُستخدم في مجموعة واسعة من المجالات مثل التسويق، والرؤية الحاسوبية، وتحليل البيانات الجغرافية.
التحديات التي تواجه الخوارزمية
بالرغم من فعاليتها، تواجه K-Means بعض التحديات، ومنها:
-
اختيار عدد العناقيد KK:
يؤدي اختيار عدد غير مناسب للعناقيد إلى نتائج ضعيفة، ما يجعل تحديد القيمة المثالية لـ KK مهمة معقدة. -
الحساسية للقيم الأولية:
النتائج تعتمد على الوسائط الأولية المختارة بشكل عشوائي، مما قد يؤدي إلى حلول محلية غير مثالية. -
الحساسية للقيم المتطرفة:
تؤثر البيانات الشاذة على الوسائط، ما يقلل من دقة النتائج. -
افتراض الشكل الكروي للعناقيد:
تعمل الخوارزمية بشكل أفضل مع البيانات التي تتوزع بشكل كروي، ولكنها قد تفشل مع البيانات ذات الأنماط غير المنتظمة.
اقرأ أيضا:
الدليل الشامل لفهم التعلم الخاضع للإشراف
طرق تحسين الخوارزمية
يمكن تحسين أداء K-Means باستخدام استراتيجيات مثل:
- K-Means++: اختيار الوسائط الأولية بذكاء لتقليل احتمالية الحصول على نتائج ضعيفة.
- طريقة الكوع (Elbow Method): تحديد العدد الأمثل للعناقيد من خلال تحليل منحنى التباين.
- درجة الظل (Silhouette Score): تقييم جودة العناقيد بناءً على المسافة بين النقاط داخل وخارج العنقود.
التطبيقات العملية
تُستخدم خوارزمية K-Means Clustering في العديد من المجالات، مثل:
- التسويق: تقسيم العملاء إلى مجموعات بناءً على سلوكهم الشرائي أو خصائصهم الديموغرافية، مما يسهم في تحسين الحملات التسويقية.
- تحليل الصور: فصل الصور إلى مناطق بناءً على خصائص اللون أو القوام.
- التحليل المالي: تصنيف الأسهم بناءً على أنماط الأداء لمساعدة المستثمرين في اتخاذ قرارات مستنيرة.
- البيانات الجغرافية: تحليل التوزيع الجغرافي للمتاجر أو العملاء لتحديد التجمعات في مناطق محددة.
الخلاصة
تمثل خوارزمية K-Means Clustering إحدى أكثر الأدوات فعالية لتحليل البيانات وتصنيفها. ومع أنها تواجه بعض التحديات، يمكن التغلب عليها من خلال تقنيات مثل K-Means++ وطريقة الكوع. بفضل بساطتها وسرعتها، تظل هذه الخوارزمية خيارًا مثاليًا للعديد من التطبيقات العملية، مما يوفر رؤى قيمة تسهم في اتخاذ قرارات مدروسة.
الأسئلة الشائعة
ما هي خوارزمية K-Means Clustering
هي خوارزمية غير خاضعة للإشراف تُستخدم لتجميع البيانات في عناقيد بناءً على التشابه بين النقاط.
كيف تعمل خوارزمية K-Means؟
تحدد الخوارزمية عدد العناقيد KK، ثم تختار وسائط أولية بشكل عشوائي، وتكرر عملية التعيين والتحديث حتى تستقر العناقيد.
ما هي مزايا K-Means؟
الخوارزمية بسيطة وسريعة، وتقدم نتائج واضحة وقابلة للتفسير.
ما التحديات التي تواجهها K-Means؟
تشمل التحديات اختيار عدد العناقيد KK المثالي، الحساسية للقيم الأولية والمتطرفة، والافتراض بأن العناقيد لها شكل كروي.
كيف يمكن تحسين الخوارزمية؟
باستخدام تقنيات مثل K-Means++، طريقة الكوع، ودرجة الظل لتحسين الدقة وتقليل التأثير السلبي للعوامل العشوائية.
ما هي استخداماتها العملية؟
تُستخدم في التسويق، تحليل الصور، التصنيف المالي، وتحليل البيانات الجغرافية.
ما هي طريقة الكوع (Elbow Method)؟
تقنية تعتمد على رسم منحنى يوضح العلاقة بين عدد العناقيد والتباين، ويتم اختيار KK عند النقطة التي يتباطأ فيها انخفاض التباين بشكل ملحوظ.